Research Overview

A high-level overview of our research interests

Rohan V Kashyap

List of Research Interests

  • Automatic symmetry discovery for discrete groups and matrix lie groups (Eg: permutation subgroups, rotations & translations).
  • Generative models. Eg: VAE, GAN & diffusion models.
  • Poisson Flow generative models.

Research Highlights

To give a more concrete idea of research we have done, here are some projects and papers roughly grouped together in themes.

Learning Invariances

Figure: AISTATS Poster.

Invariance and equivariance are very common inductive biases, with the ubiquitous convolutional layer being the most common example. When designing architectures, humans currently choose how many convolutional layers to use, together with parameters like filter size. Often these choices are made with a tedious trial-and-error procedure. To make the number of choices even larger, other types of convolutional layers have been developed in recent years, which help generalisation across different scales and rotations. The optimal inductive bias varies by problem and dataset, so it would be nice if we had an automatic procedure for determining these.

We are developing methods that allow weights and architecture to be learned at the same time, by optimising a single objective function. In our paper titled Neural discovery of permutation subgroups (AISTATS 2023), we present a novel method to discover the underlying subgroup, given that it satisfies certain conditions.

We consider the problem of learning an H-invariant function f : X → ℝ, where X = [0,1]n ⊂ Rn and H is the unknown subgroup of Sn. In general, learning such a function is intractable. However, we show that it is possible to learn such a function, i.e., discover the underlying subgroup H, where H belongs to a certain class of subgroups. The general consequence of our analysis is that learning a H-invariant function is thus equivalent to learning a G-invariant function along with a linear transformation, given that G and H satisfy certain conditions. Our results show that one could discover any subgroup of type \(S_k(k \leq n)\) by learning an \(S_n\)-invariant function and a linear transformation given below:

Theorem [Cyclic and Dihedral subgroups]: If \(k|n\), any \(\mathbb{Z}_k\)-invariant (or \(D_{2k}\)-invariant) function \(\psi\), can be realised using a \(\mathbb{Z}_n\)-invariant (or \(D_{2n}\)-invariant) function \(\phi\) and a linear transformation, in specific, it can be realised through the following form, \[\begin{equation} \psi(x) = \left( \phi \cdot \hat{M} \right) (x) \end{equation}\] where \(\hat{M} = \begin{bmatrix} M \\ I - L \end{bmatrix}\) for some \(M, L \in \mathbb{R}^{n \times n}\).

The above result can also be extended to other classes of subgroups given as:

Theorem [Main Theorem]: Any \(H\)-invariant function \(\psi\) can be learnt through composing a \(G\)-invariant function \(\phi\) with a linear transformation \(M\), i.e., \(\psi = \phi \cdot M\) if the following conditions hold:

  1. For any \(h \in H,\) \(\exists g \in G\) such that \(M(h \cdot x) = g \cdot \left(Mx\right), \: \forall x \in X\).

  2. For any \(g \in G\) such that \(g \cdot \left(Mx\right) \in R(M)\), \(\exists h \in H\) such that \(M(h \cdot x) = g \cdot \left(Mx\right), \: \forall x \in X\), where \(R(M)\) is the range of \(M\).

A Unified Framework for Discovering Discrete Symmetries

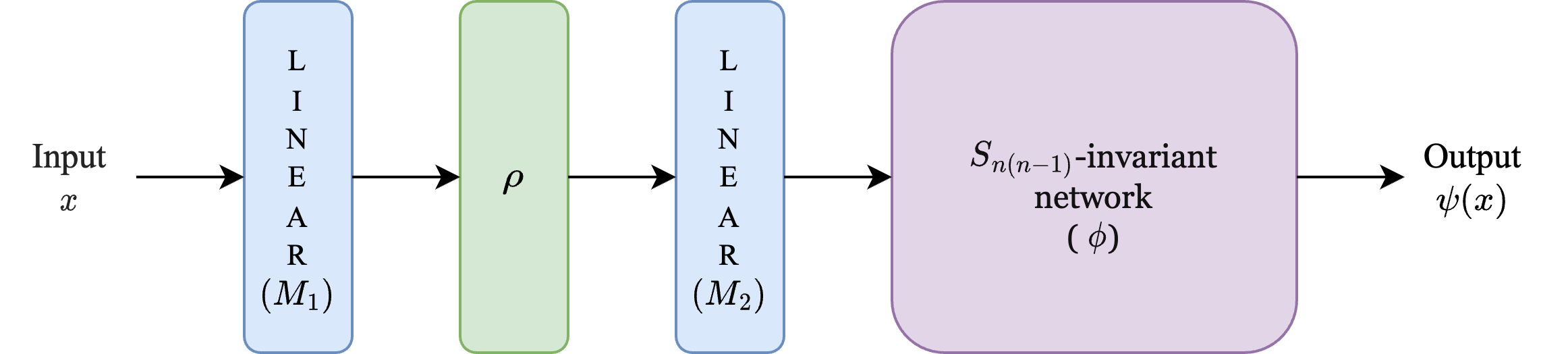
Figure: Proposed unified architecture for discovering symmetries, composed of linear transformations (\(M_1\), \(M_2\)) and nonlinear functions (\(\rho\), \(\phi\)). \(\rho\) is explicitly fixed whereas \(M_1, M_2, \phi\) are trainable. The following result guarantees that the architecture can express functions invariant to any locally symmetric, dihedral and cyclic. Here, \(\phi\) is represented by a neural network and trained using gradient descent while \(M_1, M_2\) are optimized using bandit sampling over a discrete space of matrices.

In our recent paper, A Unified Framework for Discovering Discrete Symmetries (AISTATS, under review), we propose a unified framework that enables symmetry discovery across a broad range of subgroups including locally symmetric, dihedral and cyclic subgroups. At the core of the framework is a novel architecture composed of linear and tensor-valued functions that expresses functions invariant to these subgroups in a principled manner. The structure of the architecture enables us to leverage multi-armed bandit algorithms and gradient descent to efficiently optimize over the linear and the tensor-valued functions respectively. Our main result is as follows:

Theorem [Unified symmetry discovery framework]: Let \(\mathcal{B}\) denote the class of all functions from \([0,1]^n \rightarrow \mathbb{R}\) of the form:

\[ x \mapsto \phi\left(\left[\begin{array}{l} \left(M_2 \circ \rho \circ M_1\right)(x) \\ \left(I-M_1\right)(x) \end{array}\right]\right) \]

where,

  1. \(M_1: \mathbb{R}^n \rightarrow \mathbb{R}^n\) and \(M_2: \mathbb{R}^{n(n-1)} \rightarrow \mathbb{R}^{n(n-1)}\) are linear transformations,

  2. \(\phi\) is an \(S_{n(n-1)}\)-invariant function, and

  3. \(\rho: \mathbb{R}^n \rightarrow \mathbb{R}^{n(n-1)}\) is a tensor-valued function, \(\rho:\left[x_1, \ldots, x_n\right]^T \mapsto\left[\left(x_i, x_j\right)_{i, j \in[n], i \neq j}\right]^T\).

Let \(\mathcal{I}=\left\{i_1, i_2, \ldots i_k\right\} \subseteq[n]\). Then, the following hold:

  1. Any \(S_{\mathcal{I}}\)-invariant function belongs to \(\mathcal{B}\). Moreover, the matrices \(M_1\) and \(M_2\) in its decomposition have the forms: \[ \begin{aligned} M_1[u, v] & = \begin{cases}1, & \text { if } u \in[k] \text { and } v=i_u \\ 0, & \text { otherwise },\end{cases} \\ M_2 & =I_{n(n-1) \times n(n-1)} . \end{aligned} \]
  2. Any \(\mathbb{Z}_{\mathcal{I}}\)-invariant function belongs to \(\mathcal{B}\). Moreover, \(M_1\) is of the form as given in (3) and \(M_2\) is as follows: \[ M_2[i, j]= \begin{cases}1, & \text { if } i \in[k] \text { and }\left(\rho \circ M_1\right)(x)[j]=\left(x_i, x_{\tau(i)}\right) \\ 0, & \text { otherwise. }\end{cases} \]
  3. Any \(D_{\mathcal{I}}\)-invariant function belongs to \(\mathcal{B}\). Moreover, \(M_1\) is of the form as given in (3) and \(M_2\) is as follows: \[ M_2[i, j]= \begin{cases}1, & \text { if } i \in[2 k] \text { and }\left(\rho \circ M_1\right)(x)[j]=\left(x_i, x_{\tau(i)}\right) \\ 1, & \text { else if } i \in[2 k] \text { and }\left(\rho \circ M_1\right)(x)[j]=\left(x_i, x_{\tau(i)}\right) \\ 0, & \text { otherwise. }\end{cases} \]

We remark that the above result can be extended to express functions invariant to wider classes of subgroups. The following results offer a glimpse of how this can be achieved, for instance, for product groups.

Theorem[Invariance to product groups]: Let \([n] = \bigcup\limits_{j=1}^L \mathcal{I}_j\) be a partition of \([n]\), \(G_i \in \{S_{\mathcal{I}_j}, D_{\mathcal{I}_j}, \mathbb{Z}_{\mathcal{I}_j}\}, \forall j \in [L]\) and \(G = G_1 \times G_2 \times \cdots G_L\) such that no two groups \(G_i, G_j\) are isomorphic. Let \(\psi\) be a \(G\)-invariant function, then there exists an \(S_{l}\)-invariant function \(\phi\) and a specific tensor-valued function \(\rho\), such that, \[\begin{equation} \psi = \phi \circ \rho. \end{equation}\]

Our next result shows a performance guarantee for the LinTS algorithm, showing a bound on its probability of misidentifying the optimal arm in a linear reward model.

Theorem [Error probability bound for LinTS]: Let the set of arms \(\mathcal{A} \subset \mathbb{R}^d\) be finite. Suppose that the reward from playing an arm \(a \in \mathcal{A}\) at any iteration, conditioned on the past, is sub-Gaussian with mean \(a^{\top} \mu^\star\). After \(T\) iterations, let the guessed best arm \(A_T\) be drawn from the empirical distribution of all arms played in the \(T\) rounds, i.e., \(\mathbb{P}[A_T = a] = \frac{1}{T} \sum_{t=1}^T \mathbf{1}\{a^{(t)} = a \}\) where \(a^{(t)}\) denotes the arm played in iteration \(t\). Then,

\(\mathbb{P}\left[A_T \neq a^{\star}\right] \leq \frac{c \log (T)}{T}\) where \(c \equiv c\left(\mathcal{A}, \mu^\star, \nu \right)\) is a quantity that depends on the problem instance (\(\mathcal{A}, \mu^\star\)) and algorithm parameter (\(\nu\)).

Linear Thompson Sampling (LinTS)-based bandit optimization algorithm

Observe that although the space of matrices $(M_1, M_2)$ is discrete, it is still an exponentially large set. To enable efficient search over this set, we resort to using the linear parametric Thompson sampling algorithm (LinTS). In this strategy, whose pseudo code appears in Algorithm, each possible pair of matrices $(M_1,M_2)$, denoting an arm of the bandit, is represented uniquely by a {\em binary} feature vector of an appropriate dimension $d$ (described in detail below). The reward from playing an arm with feature vector $a$ (which is the negative loss after optimizing for $\phi$ using SGD) is assumed to be linear in $a$ with added zero-mean noise, i.e., $\exists \mu^\star \in \mathbb{R}^d$ such that the expected reward upon playing $a$ is $a^{\top}\mu^{\star}$. LinTS maintains and iteratively updates a (Gaussian) probability distribution over the unknown reward model $\mu^{\star}$, and explores the arm space by sampling from this probability distribution in each round.

  1. See Automatic Symmetry Discovery with Lie Algebra Convolutional Network for a good intro. ↩︎