Research Overview

List of Research Interests

• Poisson Flow generative models.
• Variational Diffusion models.
• Direct and indirect push-forward generative models. Eg: VAE, GAN and diffusion models.
• Neural networks with invariance properties (e.g. rotation, scale, or more arbitrary) and learning invariances for continuous image manifolds.

Research Highlights

To give a more concrete idea of research we have done, here are some projects and papers roughly grouped together in themes.

Learning invariances

Invariance and equivariance are very common inductive biases, with the ubiquitous convolutional layer being the most common example. When designing architectures, humans currently choose how many convolutional layers to use, together with parameters like filter size. Often these choices are made with a laborious trial-and-error procedure (cross-validation). To make the number of choices even larger, other types of convolutional layers have been developed in recent years, which help generalisation across different scales and rotations. The optimal inductive bias varies by problem and dataset, so it would be nice if we had an automatic procedure for determining these.

We are developing methods that allow weights and architecture to be learned at the same time, by optimising a single objective function. In our paper Neural discovery of permutation subgroups (AISTATS 2023) we present a novel method to discover the underlying subgroup, given that it satisfies certain conditions. Our results show that one could discover any subgroup of type \(S_k(k \leq n)\) by learning an \(S_n\)-invariant function and a linear transformation.

A Unified Framework for Discovering Discrete Symmetries

In our recent paper, A Unified Framework for Discovering Discrete Symmetries (NeurIPS review) we propose a unified framework that enables symmetry discovery across a broad range of subgroups including locally symmetric, dihedral and cyclic subgroups. At the core of the framework is a novel architecture composed of linear and tensor-valued functions that expresses functions invariant to these subgroups in a principled manner. The structure of the architecture enables us to leverage multi-armed bandit algorithms and gradient descent to efficiently optimize over the linear and the tensor-valued functions respectively.

The following section is a brief overview of the recent advances in the theoretical analysis of push-forward generative models.

Denoising Score Matching Langevin Dynamics

Let \(p_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x}):=\mathcal{N}\left(\tilde{\mathbf{x}} ; \mathbf{x}, \sigma^2 \mathbf{I}\right)\) , \(p_\sigma(\tilde{\mathbf{x}}):=\int p_{\text {data }}(\mathbf{x}) p_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x}) \mathrm{d} \mathbf{x}\), where \(p_{\text {data }}(\mathbf{x})\) denotes the data distribution. Consider a sequence of positive noise scales \(\sigma_{\min }=\sigma_1<\) \(\sigma_2<\cdots<\sigma_N=\sigma_{\max }\). Typically, \(\sigma_{\min }\) is small enough such that \(p_{\sigma_{\min }}(\mathbf{x}) \approx p_{\text {data }}(\mathbf{x})\), and \(\sigma_{\max }\) is large enough such that \(p_{\sigma_{\max }}(\mathbf{x}) \approx \mathcal{N}\left(\mathbf{x} ; \mathbf{0}, \sigma_{\max }^2 \mathbf{I}\right)\). Song & Ermon (2019) propose to train a Noise Conditional Score Network (NCSN), denoted by \(\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, \sigma)\), with a weighted sum of denoising score matching (Vincent, 2011) objectives: \[\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg \min } \sum_{i=1}^N \sigma_i^2 \mathbb{E}_{p_{\mathrm{data}}(\mathbf{x})} \mathbb{E}_{p_{\sigma_i}(\tilde{\mathbf{x}} \mid \mathbf{x})}\left[\left\|\mathbf{s}_{\boldsymbol{\theta}}\left(\tilde{\mathbf{x}}, \sigma_i\right)-\nabla_{\tilde{\mathbf{x}}} \log p_{\sigma_i}(\tilde{\mathbf{x}} \mid \mathbf{x})\right\|_2^2\right] .\] Given sufficient data and model capacity, the optimal score-based model \(\mathbf{s}_\theta *(\mathbf{x}, \sigma)\) matches \(\nabla_{\mathbf{x}} \log p_\sigma(\mathbf{x})\) almost everywhere for \(\sigma \in\left\{\sigma_i\right\}_{i=1}^N\). For sampling, Song & Ermon (2019) run \(M\) steps of Langevin MCMC to get a sample for each \(p_{\sigma_i}(\mathbf{x})\) sequentially: \[\mathbf{x}_i^m=\mathbf{x}_i^{m-1}+\epsilon_i \mathbf{s}_{\boldsymbol{\theta}^*}\left(\mathbf{x}_i^{m-1}, \sigma_i\right)+\sqrt{2 \epsilon_i} \mathbf{z}_i^m, \quad m=1,2, \cdots, M,\] where \(\epsilon_i>0\) is the step size, and \(\mathbf{z}_i^m\) is standard normal. The above is repeated for \(i=N, N-\) \(1, \cdots, 1\) in turn with \(\mathbf{x}_N^0 \sim \mathcal{N}\left(\mathbf{x} \mid \mathbf{0}, \sigma_{\max }^2 \mathbf{I}\right)\) and \(\mathbf{x}_i^0=\mathbf{x}_{i+1}^M\) when \(i<N\). As \(M \rightarrow \infty\) and \(\epsilon_i \rightarrow 0\) for all \(i, \mathbf{x}_1^M\) becomes an exact sample from \(p_{\sigma_{\min }}(\mathbf{x}) \approx p_{\text {data }}(\mathbf{x})\) under some regularity conditions.

Push-forward generative models

Score-Based Generative Modeling (SGM) is a recently developed approach to probabilistic generative modeling that exhibits state-of-the-art performance on several audio and image synthesis tasks. Progressively applying Gaussian noise transforms complex data distributions to approximately Gaussian. Reversing this dynamic defines a generative model. When the forward noising process is given by a Stochastic Differential Equation (SDE), Song et al. (2021) demonstrate how the time inhomogeneous drift of the associated reverse-time SDE may be estimated using score-matching. A limitation of this approach is that the forward-time SDE must be run for a sufficiently long time for the final distribution to be approximately Gaussian while ensuring that the corresponding time-discretization error is controlled.

Theorem 1. Let \(g: \mathbb{R}^p \rightarrow \mathbb{R}^d\) be a Lipschitz function with Lipschitz constant \(\operatorname{Lip}(g)\). Then for any Borel set \(\mathrm{A} \in \mathcal{B}\left(\mathbb{R}^d\right)\), \[\operatorname{Lip}(g)\left(g_{\#} \mu_p\right)^{+}(\partial \mathrm{A}) \geq \varphi\left(\Phi^{-1}\left(g_{\#} \mu_p(\mathrm{~A})\right)\right)\] where \(\varphi(x)=(2 \pi)^{-1 / 2} \exp \left[-x^2 / 2\right]\) and \(\Phi(x)=\int_{-\infty}^x \varphi(t) \mathrm{d} t\). In addition, we have that for any \(r \geq 0\) \[g_{\#} \mu_p\left(\mathrm{~A}_r\right) \geq \Phi\left(r / \operatorname{Lip}(g)+\Phi^{-1}\left(g_{\#} \mu_p(\mathrm{~A})\right)\right) \text {. }\]

Let \(\nu\) be a probability measure on \(\mathbb{R}\) with density w.r.t. the Lesbesgue measure and such that \(\operatorname{supp}(\nu)=\mathbb{R}\). Assume that there exists \(g: \mathbb{R}^p \rightarrow \mathbb{R}\) Lipschitz such that \(\nu=g_{\#} \mu_p\). Let us denote \(T_{\mathrm{OT}}=\Phi_\nu^{-1} \circ \Phi\) the Monge map between \(\mu_1\) and \(\nu\), where \(\Phi_\nu\) is the cumulative distribution function of \(\nu\). Then we have \(\operatorname{Lip}(g) \geq \operatorname{Lip}\left(T_{\mathrm{OT}}\right)\).

Poisson Flow Generative Models

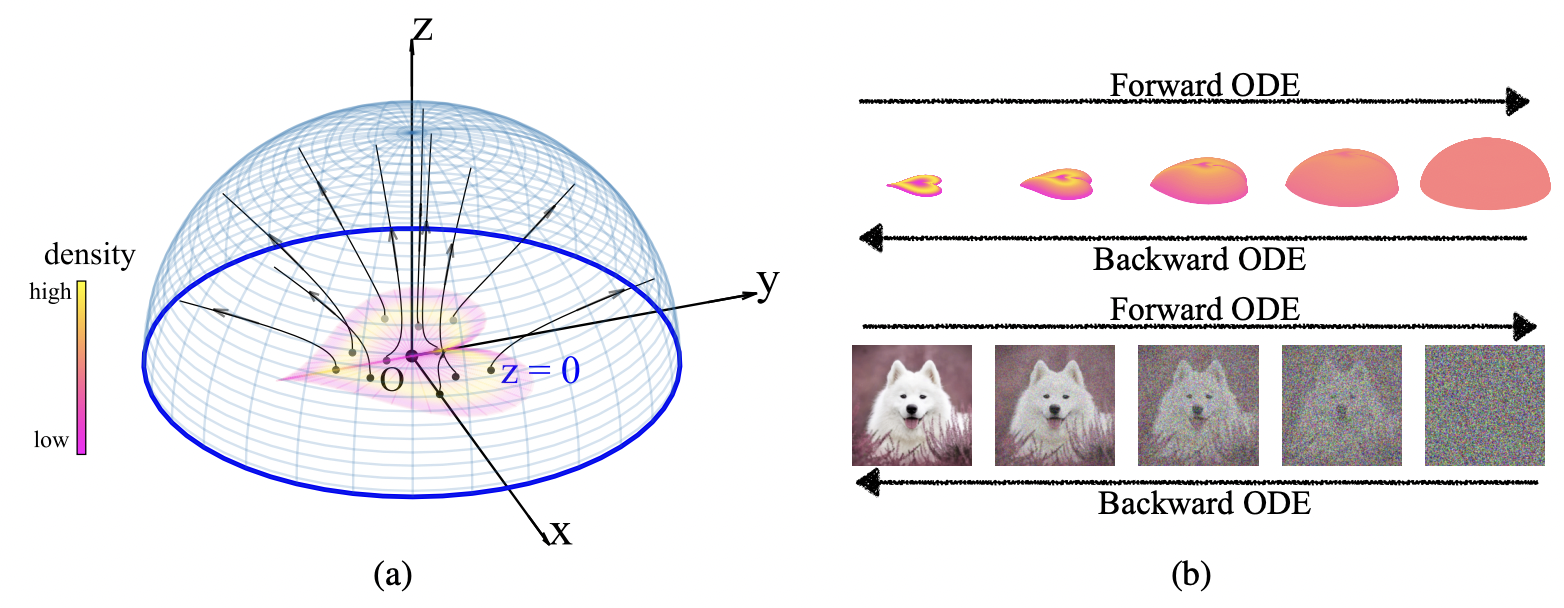
The Poisson flow generative model (PFGM) maps a uniform distribution on a high-dimensional hemisphere into any data distribution. They interpret the data points as electrical charges on the \(\mathrm{z}=\) 0 hyperplane in a space augmented with an additional dimension z, generating a high-dimensional electric field (the gradient of the solution to Poisson equation). They prove that if these charges flow upward along electric field lines, their initial distribution in the \(\mathrm{z}=0\) plane transforms into a distribution on the hemisphere of radius \(r\) that becomes uniform in the \(r \rightarrow \infty\) limit. To learn the bijective transformation, they estimate the normalized field in the augmented space.

See:

• Score-Based Generative Modeling through Stochastic Differential Equations
• Can Push-forward Generative Models Fit Multimodal Distributions?

We designed quantitative concentration bounds (using Sobolev inequalities) explicitly dependent on the number of orbits and illustrated theoretical results for incorporating invariance symmetries using Lie groups for diffusion models using a score-based formulation by utilizing the implicit structure in the time-reversed stochastic differential equations. Currently, we are working on establishing connections to compact Riemannian manifolds.

---

1. See Automatic Symmetry Discovery with Lie Algebra Convolutional Network for a good intro. ↩︎

2. Which is the case in many industrial and engineering problems. ↩︎